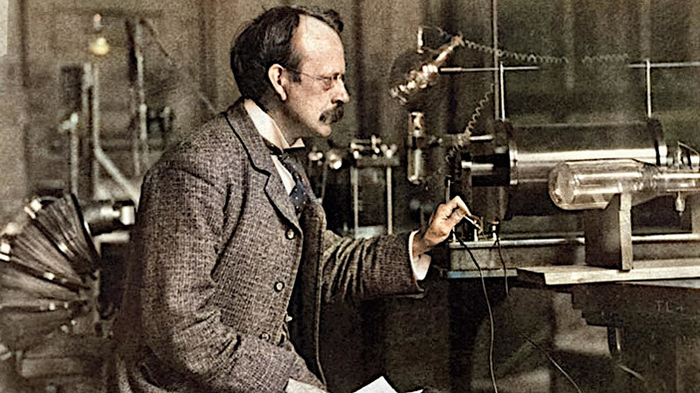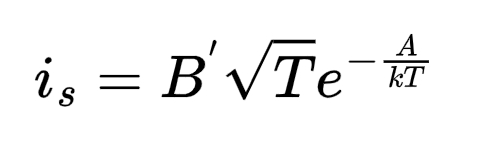Джон Томсон и его фабрика по производству нобелевских лауреатов
Между 1884 и 1919 годами серьезный на вид профессор вместе с группой талантливых студентов-исследователей в довольно скудно финансируемой Кавендишской лаборатории в Кембридже расщепил атом и положил начало новой отрасли науки, известной как физика элементарных частиц.
Профессором был Джожеф Джон Томсон (1856 — 1940) — нобелевский лауреат 1906 года и первооткрыватель электрона, но таких последствий никто не ожидал: семеро студентов-исследователей под его руководством получили Нобелевскую премию по физике и химии.
Было ли это просто причудой судьбы, что некоторые из лучших умов в области физики собрались в Кавендише в то время, или это была сверхспособность заставлять умных людей выполнять блестящую работу? Эта статья о том, как один человек смог изменить историю науки не только благодаря индивидуальному таланту, но и благодаря тщательному воспитанию выдающихся умов.
В 1884 году лорд Рэлей (Нобелевский лауреат 1904 года) ушел в отставку с поста руководителя кавендишской лаборатории физики Кембриджского университета — одного из самых престижных научных подразделений того времени. В своей записке об уходе на пенсию он рекомендовал, чтобы молодой 28-летний человек Томсон стал его заменой.
Это было беспрецедентно. На эту должность претендовало несколько высококвалифицированных и известных ученых. Несмотря на то, что Томсон был блестящим студентом с рядом публикаций на его счету и доцентом в Тринити-колледже, его квалификация физика-экспериментатора еще не были подтверждена. Некоторые недоброжелатели считали Джозефа слишком молодым, чтобы занять эту должность.
Отборочной комиссии, состоящей из лорда Кельвина, Джорджа Гэбриэла Стокса и Джорджа Говарда Дарвина — одних из лучших научных умов своего времени — предстояло сделать трудный выбор, но они всё-таки последовали рекомендации Рэлея.
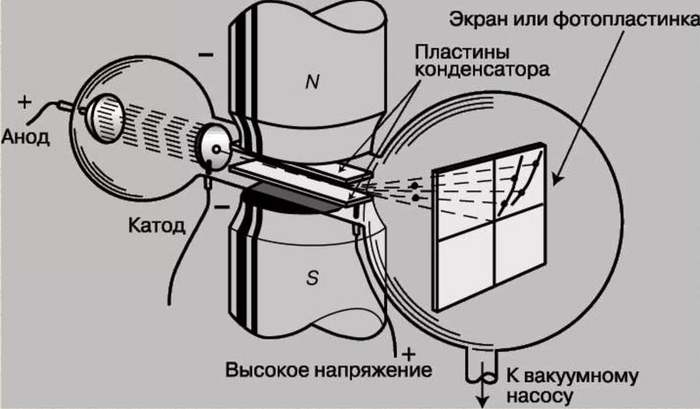
Томсон оправдал их выбор сполна, когда в серии блестяще разработанных экспериментов с электронно-лучевой трубкой (в 1897 году) дал доказательство существования электронов. Это разрушило миф о том, что атом не делим, и положило начало новой науке — физике субатомных частиц.
Томсон в своей лаборатории. Очень подробная и интересная история открытия электрона — здесь
Томсон родился в семье книготорговцев, которые финансово не могли потянуть образование сына в престижном университете. Однако, Джозефу, благодаря своим талантам, деньги были не нужны: на протяжении всего обучения он получал хорошую стипендию, ежегодно выпуская статьи в солидных научных журналах (первая была опубликована уже в 19 лет).
Томсон считал образцами для подражания знаменитого химика Далтона и физика Генри Джоуля. Однажды, когда он был совсем маленьким, кто-то из родственников спросил его, чем бы он хотел заниматься, когда вырастет, и Джозеф ответил, что хотел бы заниматься “оригинальными исследованиями”. Не многие мальчики в 1870-х годах и не многие мальчики сейчас могли бы сформулировать такие амбиции в раннем возрасте.
Томсон дома в своем кабинете в 1899 году. Он сидит в кресле, которое принадлежало Джеймсу Клерку Максвеллу, чья теория электромагнетизма до сих пор считается одним из самых замечательных достижений физики
К 50 годам Джозеф Томсон достиг всего, к чему может стремиться физик, – руководил лучшей в мире физической лабораторией, получил мировое признание за свою работу и Нобелевскую премию по физике. Он мог бы уйти на пенсию и ловить рыбу, а мир все еще помнил бы его как одного из лучших физиков всех времен.
Но есть одно достижение Джозефа, о котором не так часто вспоминают. Он был выдающимся педагогов, подобных которому мир не видел. Ряд первоклассных ученых получили свое раннее образование у Томсона — 75 его учеников занимали профессорские должности примерно в 55 университетах по всему миру, 27 были избраны членами королевского общества, а 7 его учеников стали Нобелевскими лауреатами. Последнее достижение до сих пор не повторил ни один ученый в мире!
Томсон всегда признавал, что ему повезло иметь очень одаренных учителей, которые распознали и отточили навыки молодого человека в математике и физике. Этот подход Джозеф как учитель воспроизводил для своих учеников с впечатляющим эффектом. Он ежедневно проверял успехи молодых исследователей в своей лаборатории и часто вносил свои предложения.
Один из его бывших студентов говорил “Нам всем нравилась его характерная улыбка, и каждый из нас чувствовал удовольствие, услышав шаги, которые, как знал каждый, принадлежат Томсону”. Среди его учеников-лауреатов Нобелевской премии такие люди, как Резерфорд, Астон, Уилсон, Брэгг, Баркла, Ричардсон и Эпплтон — ученые, которые заложили важнейшие кирпичики физики элементарных частиц.
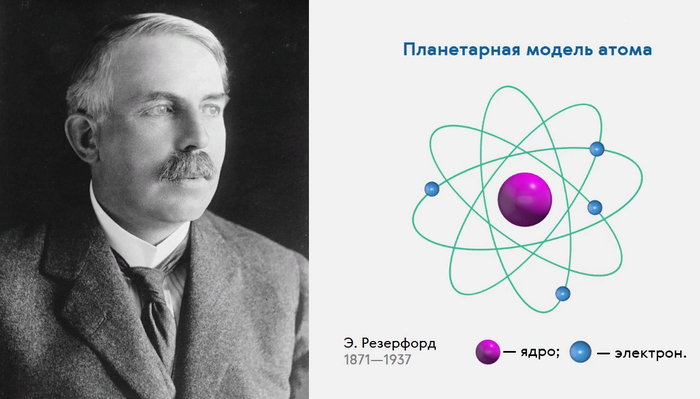
❯ Эрнст Резерфорд (1871 — 1937)
Самый известный ученик Дж. Дж. Томсона — Эрнст Резерфорд — автор прорывной планетарной модели атома. Лауреат Нобелевской премии 1908 года по химии Резерфорд родился в Новой Зеландии. В кавендишскую лабораторию он попал во много благодаря управленческим решениям Томсона, который в 1885 году смягчил правила и разрешил перспективным студентам без базового кембриджского диплома проводить исследования в лаборатории.
Резерфорд был в числе первой группы зарубежных исследователей, которым в 1895 году разрешили работать в Кавендише. В первые дни эта «новая поросль» столкнулась с крайней враждебностью со стороны кадровых ученых лаборатории. Однако именно поддержка Томсона позволила Резерфорду сосредоточиться.
Примечательно, что нобелевскую премию Эрнст Резерфорд получил вовсе не за описание модели атома, а за исследование механизмов радиоактивного распада, что привело к открытию альфа-, бета-, гамма-излучения и инертного газа радона. После признания в 1908 году нобелевским комитетом его заслуг в области «исследования распада элементов и химии радиоактивных веществ» Резерфорд продолжил плодотворно работать и сделал множество открытий в физике элементарных частиц.
В 1919 году Резерфорд сменил своего учителя на посту руководителя кавендишской лаборатории. Последнее пристанище оба, кстати, наши в Вестминстерском аббатстве по соседству с другим кембриджским гением — Исааком Ньютоном.
❯ Фрэнсис Вильям Астон (1877 — 1945)
Томсон всегда был в поиске талантов и лично убеждал перспективных студентов работать в лаборатории. Одним из таких студентов был Фрэнсис Уильям Астон, которого переманили в Кавендиш для исследования анодных лучей.
Прошлое место работы Астона — Бирмингемский институт, где он трудился под руководством Пойнтинга (с ним знакомы те, кто помнят одноименный вектор из школьной физики)
Основные исследования Астона были направлены на изучение изотопов — разновидностей атомов химического элемента, имеющие разные массы. Работа привела к созданию учителем и учеником масс-спектрографа — устройства, которое позволило Астону уже у 1919 году обнаружить 212 природных изотопов различных элементов.
На заряженную частицу, движущуюся в магнитном поле, действует сила Лоренца, искажающая ее траекторию. Определяя разницу траекторий ионизированных атомов, движущихся в магнитном поле, можно делать выводы о соотношении массы и заряда иона.
Астон был удостоен Нобелевской премии в 1922 году за «сделанное им с помощью им же изобретенного масс-спектрографа открытие изотопов большого числа нерадиоактивных элементов и за формулирование правила целых чисел». После этого он еще несколько раз модернизировал устройство.
❯ Чарльз Томсон Вильсон (1869 — 1959)
Шотландский физик, который в начале планировал стать врачом, попал под крыло Томсона в 1892 году.
Через пару лет, наблюдая атмосферные эффекты в обсерватории на горе Бен-Невис (Шотландия), Вильсон приступил к попыткам воспроизвести их в лаборатории.
Корона (слева) и глория (справа) — это оптические явления, обусловленные дифракцией света на капельках воды. Кстати, в Китае глорию называют «светом Будды». Цветное гало всегда окружает тень наблюдателя, что часто толковалось как степень его просветления (приближённости к Будде и другим божествам).
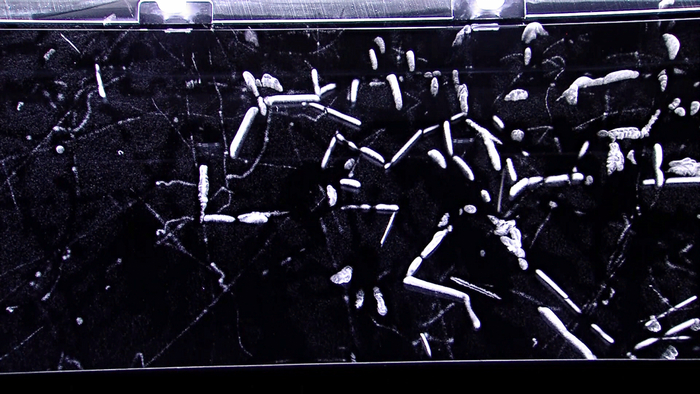
Исследования привели его к разработке облачной камеры, которая позволила отслеживать каждую отдельную субатомную частицу на фотографической пластинке. Камера Вильсона сделала возможными некоторые из крупнейших открытий в физике элементарных частиц, включая открытие позитронов (положительно заряженных электронов) и принесло её автору Нобелевскую премию в 1927 году.
Быстрая заряженная частица, двигаясь сквозь облако перенасыщенного пара, ионизирует его. Процесс конденсации пара происходит быстрее в местах образования ионов. Как следствие, там, где пролетела заряженная частица, образуется след из капелек воды, который можно сфотографировать. Именно из-за такого вида треков камера получила свое английское название — облачная камера
❯ Уильямс Лоуренс Брэгг (1890 — 1971)
11 ноября 1912 года Джозеф Томсон на заседании Кембриджского философского общества представил статью молодого аспиранта Уильямса Брэгга, который в кавендишской лаборатории трудился всего лишь год.
Австралийский физик, уроженец г. Аделаида. Его сломанная в детстве рука появилась на первом в истории континента рентгеновском снимке, сделанном в медицинских целях.
В статье обсуждалась новая техника рентгеноструктурного анализа, а три года спустя, в 1915 году, автору, которому тогда было всего 25 лет, была присуждена Нобелевская премия по физике. Брэгг стал самым молодым нобелевским лауреатом по физике и первым и пока единственным, кто завоевал это почетное звание вместе со своим отцом.
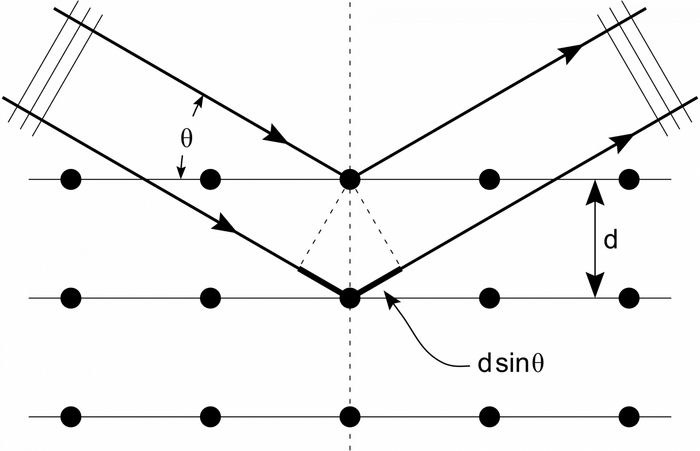
nλ = 2dsin θ — закон Брэгга-Вульфа. Точки на картинке — атомы кристаллической решетки.
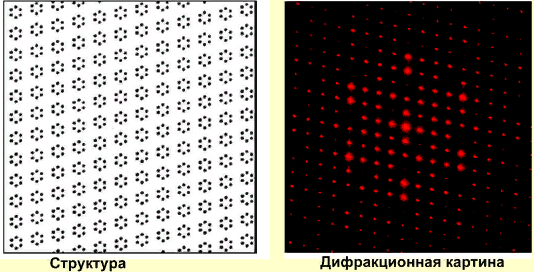
Закон Брэгга позволил по известным λ и θ рассчитать положение атомов в кристалле по дифракционной картине, которую образуют рентгеновские лучи проходя сквозь кристаллическую решётку.
Дифракционная картина получается путем измерения интенсивности рассеянных волн как функции угла рассеяния. Пики Брэгга получаются на дифракционной картине, когда углы рассеяния удовлетворяют условию Брэгга для θ и исследуемой кристаллической структуры.
❯ Чарльз Гловер Баркла (1877 — 1944)
Как и многие нобелевские лауреаты из нашей подборки, Чарльз Баркла получил образование в Тринити-колледже, а затем перешёл под крыло Джозефа Томсона в кавендишскую лабораторию.
Гловер Баркла провел там около двух лет, работая над определением скорости электромагнитных волн в различных материалах. Определяющим вкладом Баркли в науку стало открытие того, что каждый атом имеет характеристический рентгеновский спектр, на который не влияют внешние факторы, такие как температура.
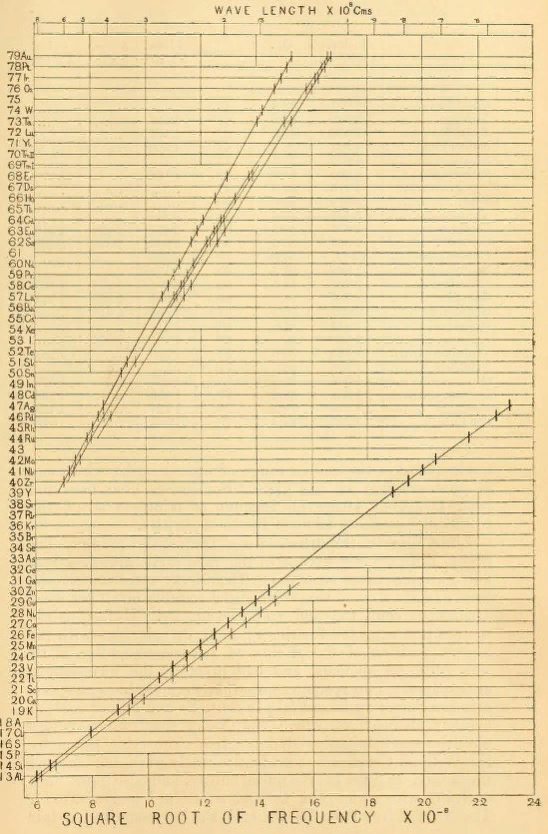
Исследования Баркли привели к т.н. закону Мозли, который вычислил конкретную формулу зависимости длины волны характеристического излучения от порядкового номера элемента. Закон удивителен тем, что это зависимость — линейная! На горизонтальной оси отмечены корень из частоты и длина волны, на вертикальной — зарядовое число.
В 1916 году Гловера Баркла отошел от дел и начала преподавать философию. Впрочем, награда всё равно нашла своего героя, и в 1917 ученый удостоился Нобелевской премии.
❯ Оуэн Уилланс Ричардсон (1879 — 1959)
Биография всех, о ком мы сегодня говорили, похожа как две капли воды: отличное школьное образование и заслуженные студенческие стипендии, которые позволили «засветиться» и попасть к Томсону. Оуэн Ричардсон — не исключение.
Биография всех, о ком мы сегодня говорили, похожа как две капли воды: отличное школьное образование и заслуженные студенческие стипендии, которые позволили «засветиться» и попасть к Томсону. Оуэн Ричардсон — не исключение.
В 1900 году он начал исследовать явление термоэлектронной эмиссии («эффект Эдисона»), заключающееся в том, что при нагревании металла электроны набирают достаточно энергии, чтобы преодолеть потенциальный барьер.
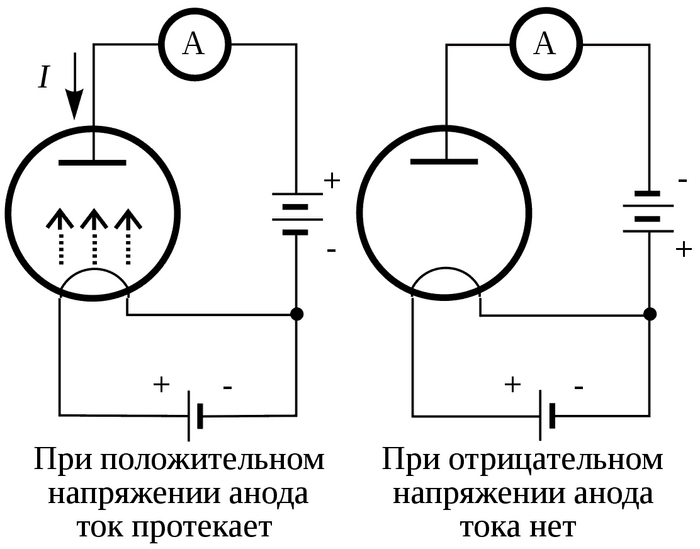
Термоэлектронная эмиссия в электровакуумном диоде. При подаче положительного напряжения на анод через вакуум между катодом и анодом протекает электрический ток, при обратной полярности напряжения тока нет. Стрелками показано направление движения электронов, направление тока обратно направлению движения электронов.
Вот только Эдисон смог подтвердить термоэлектронную эмиссию на опытах, а Ричардсон придал ей статус строгого физического закона. Конечно, у Оуэна было преимущество — благодаря своему учителю он знал, что существуют электроны.
Оказалось, что при увеличении анодного напряжения сила тока возрастает до некоторого максимального значения, при котором ток называется током насыщения, и далее не увеличивается при последующем повышении напряжения на аноде.
Ток насыщения пропорционален квадрату температуры, k — постоянная Больцмана, А и В' — параметры, зависящие от материала катода и определяющие его способность к термоэлектронной эмиссии
Именно за эту формулу Ричардсон и получил в 1928 году Нобелевскую премию, а явление термоэлектронной эмиссии привели к небывалому развитию электровакуумных приборов, которые затем использовались в качестве выпрямителей переменного тока.
Кенотроны — выпрямительные электровакуумные устройства, работающие по принципу термоэлектронной эмиссии. До сих пор можно встреть у любителей «ламповой музыка». Их несомненное достоинство — отсутствие искажений, присущих полупроводниковых устройствам.
❯ Эдуард Виктор Эплтон
Эплтон получил Нобелевскую премию в 1947 году — уже после смерти своего учителя и руководителя кавендишской лаборатории.
В лаборатории Эдуард активно взаимодействовал с Вильсоном, узучая атмосферные явления, но цель исследования была другой. Эплтон интересовался устройством атмосферы, а именно её загадочным слоем, который оказывал сильное влияние на распространение коротковолновых радиосигналов.
Опыты Маркони в 1902 году показали, что распространение КВ-радиоволн возможно не только в пределах прямой видимости, но и через переотражения от некоего атмосферного слоя, что позволяло принимать радиосигналы на другой стороне земного шара
Английский физик Оливер Хевисайд в 1902 году предположил наличие ионизированного слоя в атмосфере. Его теория включала в себя возможность распространения радиосигнала вокруг Земли, несмотря на её кривизну. Независимо от Хевисайда эксперименты по дальнему приёму коротких волн через Атлантику между Европой и Америкой проводил американский инженер-электрик Артур Кеннели. Они предположили, что где-то вокруг Земли существует ионизированный слой атмосферы, способный отражать радиоволны. Его назвали слоем Хевисайда — Кеннели, а затем — ионосферой.
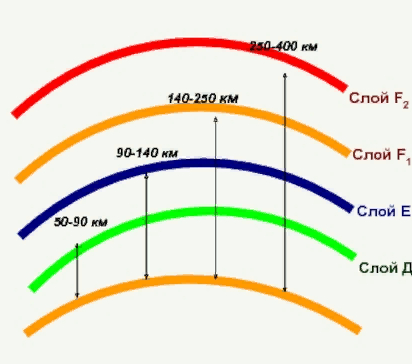
Слой Д ионосферы практически полностью поглощает радиосигналы, слой E — способен отражать длинные и средние волны, а слой F — имеет максимальную ионизацию и используется для работы на коротких волнах
Именно за открытие слоя F (на западе его часто называют слоем Эплтона) физик получил заслуженную награду. В серии экспериментов было определено, что он расположен на высоте 300-400 км над поверхностью Земли. Методика, которую Эплтон использовал в ходе исследований, оказала огромное влияние на развитие радиолокации.
❯ P.S.
В своей статье я рассказал про 7 нобелевских лауреатов, которые достигли вершины научной карьеры под руководством Томсона. Однако, есть еще один великий ученый, к которому Джозеф имеет непосредственное отношение. Это его сын — Джордж.
В то время, как отец подтвердил существование электрона как отдельной частицы (корпускулы), сын доказал, что электрон имеет волновые свойства, что стало первым экспериментальными доказательством принципа корпускулярно-волнового дуализма, сформулированном де Брейлем в 1920 году. Нобелевку за это открытие Джордж получил еще при жизни отца — в 1937 году.